Resolution of Generic Safety Issues: Issue 198: Hydrogen Combustion in PWR Piping ( NUREG-0933, Main Report with Supplements 1–35 )
DESCRIPTION
Historical Background
This issue was initiated1833 in response to a recommendation in the screening analysis of Generic Issue (G)I-195, "Potential Hydrogen Combustion in BWR Piping." GI-195 investigated the potential safety significance of hydrogen combustion events that had actually occurred in BWR primary system piping. Although no similar events had been observed in PWRs, it was felt that the potential safety significance of such events in PWRs should also be investigated.
Safety Significance
In any water-cooled reactor, radiolysis of the water in the reactor core is always producing some elemental hydrogen and oxygen. In the BWR experience described in GI-195, these gases, because of their buoyancy in a steam atmosphere, tended to build up in high, stagnant points in the primary system over a period of time. This hydrogen-oxygen mixture, although somewhat diluted by steam, is also at reactor operating conditions, i.e., at a pressure of about 1000 psi and a temperature near 500F. At these conditions, relatively little energy is required to ignite the mixture. There were three events where a combustible mixture built up in piping connected to the primary system and detonated. Although the gas buildup in all three cases was in a pipe volume isolated from the primary system by a check valve, the force of the detonations was sufficient to rupture the piping. In three other events, a combustible mixture accumulated in the top works of a safety/relief valve. When the mixture ignited, mechanical damage caused the valves to fail open and blow down the primary system.
The screening analysis of GI-195 concluded that the frequency of such events was sufficiently low that, given the many diverse systems available to mitigate such an event in BWRs, there was insufficient safety significance to justify regulatory action on BWRs. However, the review panel noted that, although a search of PWR operational history found no such events, PWRs also do not have as many ways of mitigating a loss of coolant accident. Because of this, the panel recommended that the hydrogen combustion phenomenon also be investigated for PWRs.
SCREENING ANALYSIS
Although there have been hydrogen fires at PWR plants, particularly during maintenance activities, no events which occurred in the primary system at power have been reported. Therefore, some deterministic methods must be used to estimate where such events are likely, and how frequently they might occur.
The PWR primary system is a closed system. In order to limit corrosion, it is common practice to operate with an excess of dissolved hydrogen in the primary coolant, which has the effect of scavenging the oxygen produced by radiolysis. This is accomplished by providing a hydrogen cover gas in the volume control tank in the Chemical and Volume Control System (CVCS), which supplies charging fluid to the primary system. Normally, dissolved oxygen is maintained below 0.1 ppm, and dissolved hydrogen will be in the range of 25 to 35 cc (at STP) per kilogram of water, which is equivalent to a weight percentage of 2.2 to 3.1 ppm.
Deflagration or detonation of a hydrogen-oxygen mixture could occur if a gas bubble formed in the primary system and was trapped in a stagnant volume in the upper portion of the system (e.g., the control rod travel housings, the reactor vessel head vent, or any other upward-leading pipe that normally carries no flow). Alternatively, the gases could accumulate in the pressurizer steam space. At pressures around 2000 psi and temperatures approaching 600F, relatively little energy would be needed for ignition.
Phenomenology
A review of the physical phenomenology of gas solubility and bubble formation is helpful here. A more complete description can be found in NUREG/CR-2726.1872 Consider a volume containing liquid water and hydrogen gas, in equilibrium with pressure P and temperature T. There will be some hydrogen gas dissolved in the liquid phase in the lower portion of the volume, and some water vapor in the gas phase above.
According to Henry's Law, the solubility of hydrogen is proportional to the partial pressure P(H2) in the cover gas.
![]()
Where P(H2) = partial pressure of hydrogen
H(T) = Henry's Law constant
X(H2) = mole fraction of hydrogen in the liquid phase.
The total pressure is the sum of the partial pressure of hydrogen and the partial pressure of the water vapor, which is just the saturation pressure for water at temperature T.
P = P(H2) + PSat (T)
For example, consider the conditions at the top of a PWR reactor vessel, above the core. From the PWR training manual,
P = 2235 psig = 2250 psia
T = 610.7F = 321.5C = 594.66K
H(T) = 1.25E5 psia/mole fraction1872
At this temperature, the saturation pressure of water is
P(sat) = 1667.8 psia
The partial pressure of the hydrogen is the total pressure minus this saturation pressure:
P(H2) = 2250 - 1667.8 = 582.2 psia
Then, using Henry's Law,
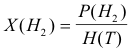
Working this out, X(H2) = 582.2 psia/1.25E5 psia/mole fraction = 4.66E-4 mole fraction, which works out to about 515 ppm by weight.
This is the equilibrium concentration. If more hydrogen is added to form a higher concentration, the solution would be supersaturated, and the excess hydrogen would bubble out in the gas phase. Conversely, if the hydrogen concentration in the liquid water were below 515 ppm, the gas bubble would dissolve into the liquid. Since the normal reactor chemistry maintains the hydrogen concentration below 3.1 ppm (about 0.6% of the saturation value), gas bubbles would not be expected to form in this area.
Similarly, the equilibrium concentration for oxygen is about 3560 ppm, and the normal concentration in the coolant is about 0.1 ppm (D. M. Himmelblau, "Solubilities of Inert Gases in Water," Journal of Chemical & Engineering Data, 5:10-15, 1960). Clearly, oxygen is even less likely to come out of solution and form a bubble, since its equilibrium solubility is higher, and its normal concentration is lower. Similar calculations for various locations in the primary system result in the following equilibrium concentrations:
| Location | Pressure(psia) | Temperature, (F) | Equilibrium hydrogen concentration (ppm) | Equilibrium oxygen concentration (ppm) |
|---|---|---|---|---|
| Reactor vessel head, nominal conditions | 2250 | 610.7 | 515 | 3560 |
| RCS cold legs & vessel downcomer | 2250 | 545.7 | 323 | 2150 |
| Control rod drive travel housings | 2250 | 248 | 340 | 1980 |
| Pressurizer | 2250 | 653 | essentially zero | essentially zero |
| Volume Control Tank (one atm. H2 overpressure) | 30 | 115 | 3.5 | --- |
Again, given that the normal hydrogen concentration is 2.2 to 3.1 ppm, and normal oxygen concentration is 0.1 ppm, gas bubbles are not expected to form in the normally liquid-filled portions of the primary system. If such bubbles were somehow introduced, they would be expected to dissolve into the liquid coolant over a period of time. Therefore, collection and detonation of these gases in the liquid-filled portion of the primary system do not appear to be credible.
The exception is the pressurizer steam space. In theory, if the pressure were exactly equal to the saturation pressure for water at that temperature, the partial pressure of hydrogen (and oxygen) would be zero and any dissolved gas would be driven out of solution until some partial pressure of hydrogen and oxygen existed in the steam space. For 3.1 ppm, this translates to a partial pressure of 2.27 psia of hydrogen in the pressurizer steam space, if the gas were evenly dispersed. For a nominal steam volume of 720 cubic feet, this is equivalent to 62 moles of hydrogen gas, which, at 2250 psia and 653F, would occupy a bubble approximately 14 inches in diameter if collected into one volume.
Similarly, if the oxygen concentration in the liquid coolant is 0.1 ppm, the partial pressure at equilibrium conditions would be 0.00647 psia, implying the presence of slightly less than six grams of (uniformly dispersed) oxygen in the steam space. If gathered together in one volume, this is equivalent to a bubble approximately two inches in diameter.
However, the hydrogen and oxygen are less dense than steam at the same temperature. The densities work out as follows:
Hydrogen gas 0.38 lb/ft3. (Based on ideal gas law)
Oxygen gas 6.02 lb/ft3. (Based on ideal gas law)
Saturated steam 6.373 lb/ft3. (Based on steam tables)
Depending on the degree of stagnation in the pressurizer steam space, these gases, because of their buoyancy, will tend to collect at the top of the pressurizer steam space, rather than being evenly distributed. If the mixture of gases is quiescent, with no turbulence or convection currents, the hydrogen will rise to the top. The oxygen is less buoyant, but will still tend to rise and form a layer at the interface between the hydrogen and the steam. This will tend to reduce the partial pressure of both gases at the liquid surface, causing more gases to come out of solution. Because more dissolved hydrogen (and oxygen) is continuously being introduced into the primary coolant, the collection of a significant amount of these gases at the top of the pressurizer steam space does appear to be credible. Moreover, because of the tendency to stratify, there will be a locus somewhere in the hydrogen/oxygen interface where the ratio of the two gases permits deflagration.
Conversely, if this volume has enough circulation to remain well mixed, the hydrogen and oxygen will be highly diluted in steam, and are unlikely to form a combustible mixture in this volume. However, even if this volume is well-mixed, any connected piping can still collect pockets of hydrogen and oxygen if this piping leads in an upward direction and is slightly cooler than the main pressurizer steam space. The two combustible gases will tend to rise and collect in the upper portions of the piping, and the steam will tend to condense on the pipe walls and run back into the main volume.
In reality, the pressurizer steam space is likely to have some convection currents whenever the heaters are in operation. Also, normally a small amount of flow is maintained in the spray line to keep the boron concentration in the liquid-filled pressurizer volume equal to that in the rest of the reactor coolant system. Thus, there is likely to be some mixing, such that the hydrogen and oxygen are unlikely to be present in well-defined, horizontal layers, but the presence of a combustible mixture, particularly in attached piping, cannot be ruled out.
The top of the pressurizer does have some locations where collection and ignition of a hydrogen-oxygen mixture could pose a problem. For a typical Westinghouse design, these include:
- The top of the head itself. However, detonation of a gas stratum here would not be likely to do much damage, since the gas volume would not be confined.
- A bolted personnel access hatch ("manway"). Again, detonation of a gas stratum here would not be likely to do much damage, since the gas volume would not be confined.
- The pressurizer spray nozzles (supplied by a four-inch line), which are located at the top of the upper head in the Westinghouse design. However, normal operational practice is to maintain a small flow through these lines all the time, in order to ensure a uniform boron concentration throughout the primary system. Thus, the line is normally liquid-filled, which greatly reduces the likelihood of noncondensible gases accumulating in this volume.
- Safety Valves: These are connected via 6-inch pipes, but the pipes are shaped in the form of a loop seal, keeping liquid in contact with the valve seat. (In contrast to the case of BWRs, catalysis by the plating in the valve internals is not possible.) The only volume which can accumulate gases is in the pipe upstream of the loop seal. A rupture of one of these lines would be an "intermediate" (i.e., up to six-inch equivalent diameter) LOCA.
- PORV Lines (Including Block Valves): The PWR training manual lists this as a six-inch line. However, the PORV capacity varies significantly from plant to plant, and presumably this pipe size can vary as well. However, a six-inch equivalent diameter LOCA should bound any PORV line break for any plant.
- Various instrument taps and small pipes, such as the level instrumentation, sampling lines, valve leakoffs, etc. A rupture of one of these lines would be a small break LOCA.
The design specifics can vary from product line to product line, and from reactor vendor to reactor vendor. For example, some B&W pressurizers have a vent valve at the very top, and the spray line penetration is off to the side, with a pipe running inside the steam space to the spray nozzle, which is located just below the center of the upper head. Nevertheless, all designs will have similar potential break locations.
Initiating Event Frequency Estimate
According to a private communication from the IAEA, PWR experience is approximately 6280 reactor-years at the time of this writing. An examination of the IAEA database has not found any instances of hydrogen deflagration in the primary system of a PWR.
In contrast to the PWR experience, there have been six such events in approximately 2325 BWR-years, as was discussed in GI-195. Thus, the credibility of such an event in a PWR is based on the experience of BWRs. There has been no PWR event which would indicate the possibility of such an event in a PWR. Clearly, the frequency of such an event in a PWR must be much less than the frequency of occurrence in BWRs, given that no PWR events have occurred, even though the accumulated experience of PWRs is almost triple that of BWRs. It will be necessary to make some assumptions regarding the combustion phenomena in order to extrapolate the BWR experience to PWRs.
One candidate explanation for the difference of event frequencies would be the PWR practice of intentionally operating with an excess of hydrogen in the coolant, with the express purpose of reducing the oxygen concentration. However, many BWRs use an analogous practice, adding hydrogen or noble metals to the feedwater and thereby reducing oxygen concentrations to as low as 0.005 ppm - actually less than oxygen concentrations in PWRs. This technique was being used in the Japanese plant that experienced a rupture of a steam condensation line. (See GI-195.) Thus, the PWR hydrogen strategy does not appear to provide a viable explanation for the difference in frequencies.
There are three other major differences between the steam spaces in a BWR and in a PWR. First, the PWR pressurizer steam space operates at double the pressure of a BWR, and consequently is about 100F hotter. It is not obvious how this would affect the likelihood of a deflagration of hydrogen and oxygen. However, a higher temperature and pressure normally increase rather than decrease the likelihood of a spontaneous ignition. Thus, this difference also does not appear to provide a viable explanation for the difference in frequencies.
Second, the steam volume in a PWR pressurizer is fairly small - about 720 cubic feet. There is no readily-available data on the steam-filled volume in a boiling water reactor, but a rough calculation based on vessel dimensions, and including the steam lines, gave an estimate of approximately 7960 cubic feet - about eleven times that of a PWR. It does appear likely that more steam volume implies a higher likelihood of a combustion event. (Certainly, reducing the volume to zero would reduce the combustion probability to zero.)
Third, a PWR pressurizer does not have as many valve-isolated volumes connected to it. It should be noted that in all three BWR events that resulted in a pipe rupture, the rupture occurred in a pipe volume which was isolated by a check valve or isolation valve from the primary system. Although this (fortunately) meant that the events involved no significant coolant inventory loss, it also raises a question as to whether the pipes would have ruptured if the volume had not been confined. (Even a check valve, which would normally have relieved pressure by passing inventory back into the primary coolant system, might provide enough resistance to allow a deflagration event to transition into a detonation event.)
In the remaining three BWR events, combustible gases collected in the top works of a safety/relief valve. In these events, there was no piping rupture, but the safety/relief valve failed open. Such an event is less likely in a PWR, because of the use of loop seals, and because PWRs generally use spring safety valves which do not have the same top works as a BWR S/RV. It would be possible for a pressurizer PORV to be damaged and fail open by this mechanism, but the block valve would be available to stop the inventory loss.
Thus, the lower number of isolated volumes connected to a PWR steam space would also help explain the lower frequency of observed combustion events in PWRs.
In the absence of any better information, it will be assumed that the frequency of a combustion event in a PWR can be estimated from the BWR event frequency in linear proportion to the steam volumes of the two designs. For this purpose, the BWR safety/relief valve openings will not be included, since the analogous events in a PWR are rendered far less likely by the loop seals and the valve internals design. The BWR isolated-pipe-rupture event frequency used in the screening analysis of GI-195, based on three events in 2325 BWR-years, was 1.3E-3 event/ BWR-year, normally distributed with a standard deviation of 7.5E-5/BWR-year. Ratioing this by the steam space volumes gives an estimated PWR combustion event frequency of 1.17E-4 event/PWR-year, with a standard deviation of 6.8E-5/PWR-year.
A combustion event such as this does not necessarily lead to a loss of coolant, as the BWR experience shows. The screening analysis for GI-195 used an exponential distribution (with a mean of 0.21) to estimate the likelihood of a non-isolatable pipe rupture, given a combustion event. It should be noted that this is not a distribution with a peak at 0.21. Instead, this distribution has a maximum value at zero, a mean of 21%, and a tail that is "chopped off" with a value of 0.04 at unity.
In the absence of any better information, this same exponential distribution will be used in this analysis. However, it should be noted that, in the BWR screening analysis, this distribution was primarily a geometrical parameter used to describe the likelihood that a pipe rupture would be in a location not isolatable, i.e., the complementary likelihood would be the likelihood of a rupture in an isolatable location. In the present use for a PWR scenario, this is the likelihood that a combustion event will result in coolant inventory loss. The complementary likelihood is that of a combustion event that causes no significant damage.
Before going further, an examination of the reasonableness of these numbers is in order. Given that there are currently 6280 PWR-years of experience worldwide, and no observed events, it is reasonable to expect frequencies that are less than 1/6280, or about 1.6E-4. However, estimates that are several orders of magnitude less than this upper limit would need considerable justification.
The mean PWR combustion event frequency distribution above is 1.17E-4/PWR-year, estimated from the BWR experience. This is not much less than what would be estimated if an actual event had been observed in the existing 6280 PWR-years of experience, which would be about 1.59 event/PWR-year. Thus, the estimate extrapolated from BWR experience is not highly non-conservative.
However, it could be argued that PWR combustion events might already have occurred but not have been noticed. To address this, a numerical calculation of the frequency of pipe ruptures was performed, using the normal combustion event frequency distribution and the exponential pipe rupture probability distribution discussed above. The results were a mean estimated pipe rupture frequency of 2.47E-5 event/PWR-year. (The number of significant figures does not imply accuracy to this degree, but instead are provided as an aid in following the calculation.) This is about 15% of the value corresponding to one actual event in the existing 6280 PWR-years of experience. Again, this appears to be reasonable.
Discussion
Again, there are two modeling assumptions in the approach to initiating event frequency above: that the PWR combustion event frequency can be extrapolated from the observed BWR frequency in proportion to steam space volumes, and that the likelihood that such a combustion event will result in a breach of the reactor coolant pressure boundary can be estimated by exponential assumption used in GI-195. The numerical effect of both of these assumptions will be explored in the section on "core damage frequency" below.
Both of these assumptions are being made because, if there were no BWR events, there would be no experience indicating that such an event would be expected in a PWR. There have been no recorded events of this nature in 6280 PWR-years of experience, worldwide. One other approach would be to focus only on the PWR experience and see if a bounding value can be inferred. This can be done by assuming an exponential distribution for the initiating event frequency, and choosing the exponential parameter such that 95% of the distribution lies below a frequency of one event in 6280 PWR-years, consistent with the usual use of a 95% confidence interval. This approach, which also will be explored, makes no assumptions based on BWR experience.
Core Damage Frequency
The event of interest is a breach in the reactor coolant pressure boundary caused by a detonation in the pressurizer steam space or associated piping. In view of the various pipe sizes where a combustible mixture might accumulate, the possible break sizes include:
- A very small break (S3 - 1/2 inch or less equivalent diameter) caused by a ruptured instrumentation line or a PORV leak.
- A small break (S2 - 1/2 inch to 2 inches equivalent diameter) caused by damage to the PORV and/or block valve internals.
- An intermediate-size break (S1 - 2 inches to 6 inches equivalent diameter) caused by rupture of the line leading to the PORV or by rupture of the pressurizer spray line.
Based on their positions in the upper portions of the pressurizer, the PORV and spray lines are the most credible locations, although the spray line is normally liquid-filled. Thus, the probabilistic calculation will assume an intermediate-size ("S1") break. (This is somewhat conservative, in that instrument line breaks, sampling line breaks, etc. would normally be classified as S2 LOCAs, and evaluated using a separate event tree. This screening analysis therefore is bounding in the sense that all breaks are evaluated as S1 breaks.)
The NUREG-11501081 PRA for the Sequoyah plant was chosen for the analysis. This plant has a somewhat higher vulnerability to loss-of-coolant accidents because of its manual switchover to ECCS recirculation mode, and thus should bound most PWR plants.
As was done for the GI-195 screening analysis, this scenario was analyzed by constructing a new event tree. This new event tree was a simple copy of the existing event tree for the intermediate break "S1" LOCA, but the initiating event at the beginning of the tree was replaced by two top events - the detonation-induced pipe break frequency followed by the probability of not isolating the break, as described in the paragraphs above. The remainder of the event tree is exactly the same as that for the "S1" LOCA.
Five separate cases were run, to test first the event tree itself, and then to explore the effect of the various modeling assumptions described earlier. Case I was intended to see if the results of the calculation would match the published results for the SI LOCA event in the NUREG-11501081 analyses. To do this, the initiating event frequency was set to 10-3 S1 LOCA event/year, the probability of a non-isolatable break was set to unity, and the calculation was run using a sequence cutoff frequency of 10-7 and limited Latin hypercube sampling. The result was a mean core damage frequency (CDF) of 6.86E-06/year. The mean S1 LOCA sequences given on pp. 5-16 and 5-17 of NUREG/CR-4550,1318 Vol. 5, Part 1, Rev. 1, sum to 6.8E-06, which compares quite well.
The sequence cutoff of 10-7 which was used in the NUREG-11501081 PRAs made the calculation much more practical by greatly reducing the number of cut sets to be calculated. Although such a cutoff tends to slightly reduce the CDF estimate, this is an appropriate numerical technique for the original PRA, since the S1 sequences contributed less than 10% of the total CDF. However, the sequences of interest for this GI are quite likely to be in the 10-7 range, and using this cutoff would significantly affect the results. Therefore, Case II is a repeat of Case I, i.e., a calculation of the S1 LOCA tree, but with the cutoff frequency lowered to 10-10/year, and using regular Monte Carlo sampling instead of the limited Latin hypercube method.
Case III is the same event tree, but with the initiating event frequency lowered to 1.17E-4/PWR-year, the estimate derived from BWR experience, and the probability of a non-isolatable break still set to unity. This calculation is not a "test case" like the first two cases, but instead corresponds to a CDF associated with this GI, although it assumes that every combustion event causes a LOCA.
Case IV is similar to Case III, but this time the probability of a non-isolatable break is calculated by means of the exponential distribution described earlier. This case is the "best" estimate of the safety significance of the GI, based on extrapolation from the experience in BWRs.
Finally, Case V uses the limiting exponential initiating event frequency based only on PWR experience, with the probability of a non-isolatable break set to unity. This case is intended as a check on the modeling assumptions used in Cases III and IV. The results of these cases are as shown in Table 3.198.1.
(Results in this and in subsequent tables are given to three significant figures for the convenience of the reader who wishes to follow the calculations, and are not intended to imply that these parameters are known to this accuracy, as the percentile range given in the table itself clearly shows.)
As can be seen by comparing the various cases tabulated above, the "limiting" case V CDF is only about a factor of two greater than that estimated by Case IV. Also, the effect of the rather questionable extrapolation of pipe break probability given an ignition event can be seen by comparing the mean estimates based on Case IV vs. Case III: this assumption reduces the calculated CDF by about a factor of five. More importantly, all three cases associated with this GI (i.e., Cases III, IV, and V) have core damage frequencies below the GI screening criterion 10-6 core damage event/RY.
In addition, an audit calculation was performed using a SPAR model for a PWR with the highest CDF for the medium LOCA. (A description of this calculation is attached to this report.) The audit calculation is similar to Case V, in that it is based on the PWR data only, but uses a more sophisticated Bayesian approach. This calculation gave a mean CDF of 8.3E-7, which agrees quite well with Case V above, and also is below the GI screening criterion of 10-6 core damage event/RY.
Table 3.198-1
| Calculation | Mean | 5th Percentile | Median | 95thPercentile |
|---|---|---|---|---|
| Case I existing S1 initiating event frequency, cutoff = 10-7, LHS sampling | 6.860E-06 | 1.645E-07 | 1.931E-06 | 2.770E-05 |
| Case II Existing S1 initiating event frequency, but cutoff = 10-10 and Monte Carlo sampling | 1.003E-05 | 1.982E-07 | 2.415E-06 | 3.259E-05 |
| Case III Initiating event frequency set to ratioed BWR ignition frequency, but assuming every ignition causes a break | 1.232E-06 | 1.327E-07 | 7.018E-07 | 3.344E-06 |
| Case IV Initiating event frequency set to ratioed BWR ignition frequency and including non-isolatable break probability | 2.425E-07 | 4.413E-09 | 9.520E-08 | 8.662E-07 |
| Case V Initiating event frequency set to 95% confidence distribution based on PWR experience. | 5.113E-07 | 1.614E-08 | 2.354E-07 | 1.680E-06 |
Consequence Estimate
In the base PRA, the S1 LOCA sequences were placed in Plant Damage State Group 2 (see NUREG/CR-4551,1795 page 2.9). A rough estimate of the consequences was made, using the CRIC-ET Code1796 and the Sequoyah model, but using a consequence file loaded with the GIs program standard site parameters. The results, using the NUREG-11501081 technique of limited Latin hypercube sampling of 200 samples, were as follows:
| Person-rem per reactor-year | |
| Mean | 0.14 |
| 5th percentile | 1.15E-03 |
| 95th percentile | 0.813 |
| Median | 2.59E-02 |
The distribution is based on the uncertainties associated with the Level II and Level III analyses, and does not include the Level I distribution. (Again, the results in this table are given to three significant figures for the convenience of the reader who wishes to follow the calculations, and are not intended to imply that these parameters are known to this accuracy, as the percentile range given in the table itself clearly shows.) These estimates are well below the screening cutoff of 100 person-rem/RY given in the Handbook for Management Directive (MD) 6.4.
Large Early Release Frequency (LERF)
The NUREG-11501081 models loaded into the CRIC-ET code precede the development of large early release models, such as those described in NUREG/CR-65951873 Nevertheless, an approximation can be made using the CRIC-ET code by selecting accident progression sequences which involve a large release. For this analysis, the following were selected:
| Accident progression characteristic | Description | Mean frequency | Expected early fatalities, conditional on event |
|---|---|---|---|
| 1C | Containment failure during core degradation | 1.47E-08 | 10.9 |
| 1D | Containment failure at vessel breach | 3.11E-08 | 17.9 |
| 6A | Induced Steam Generator Tube Rupture | 1.20E-10 | 28.6 |
| 10C | Containment failed due to small hole, leak, failure to isolate | 3.78E-08 | 0.77 |
| Combination | all above sequences | 6.74E-08 | --- |
The frequencies and conditional early fatalities were calculated using the CRIC-ET code and the standard Generic Issues Program site parameters. Other accident progression sequences either were not applicable to a LOCA-initiated event (e.g., characteristics 1A and 1B are vessel rupture failures), or were not large and early, and (not surprisingly) had an estimated number of early fatalities below 0.5. The "combination" result in the bottom row is not a simple sum of the other rows, since there are some sequences which would be included in more than one row.
The combination row is a reasonable approximation for LERF. The statistical distribution is:
mean 6.74E-08 large early releases/RY
5th percentile 1.34E-09
95th percentile 2.92E-07
median 2.18E-08
The distribution is based on the uncertainties associated with the Level II and Level III analyses, and does not include the Level I distribution. Again, the mean is well below the screening cutoff of 10-7 large early release/RY given in the Handbook for MD 6.4.
Cost Estimate
Because of the low CDF and risk, a cost estimate will not affect the conclusion of this analysis. Therefore, no cost analysis was performed.
Uncertainties
One of the more unusual aspects of the screening analysis calculations for this GI is that the initiating event is based on actual data, which results in an uncertainty distribution which, although quite wide by experimental standards, is much smaller than the uncertainty limits often seen in probabilistic analyses. Also, the distribution is normal rather than log-normal. The effect is to produce an estimate of CDF where the uncertainty bounds are not as wide as usual. However, some caution is called for in understanding these uncertainty limits, since they do not include the modeling uncertainty associated with extrapolating BWR experience to PWRs.
Discussion
The estimates above are all predicated on the fact that no hydrogen combustion events have thus far been observed thus far in PWRs. If such an event does occur in the future, this GI should be reevaluated. Similarly, if more BWR events occur, such that the estimated BWR initiating event frequency increases above the current estimate of 1.3E-3 combustion event/BWR-year, this GI should be reevaluated.
CONCLUSION
The CDF, LERF, and risk associated with this GI are below the screening thresholds given in Appendix C of the Handbook for MD 6.4, "Generic Issues Program." Therefore, it was concluded that there was insufficient justification for this GI to continue to the technical assessment stage, and the issue was DROPPED from further consideration.1874
REFERENCES
|


