Resolution of Generic Safety Issues: Issue 141: Large Break LOCA with Consequential SGTR ( NUREG-0933, Main Report with Supplements 1–35 )
DESCRIPTION
Historical Background
Large-break loss-of-coolant accidents (LBLOCA) with consequential steam generator tube ruptures (SGTR) was identified as a GSI in a DRPS/RES memorandum1086 on April 28, 1987. The issue surfaced as a result of the proposed ECCS Rule change to Appendix K of 10 CFR 50 which would remove some of the conservatisms in calculating peak clad temperatures (PCT) following an accident. The concern in this issue is that a LBLOCA might induce SGTRs and increase the severity of the LBLOCA. This concern involves the possibility of increased core degradation, due to primary system dilution with unborated water from the secondary side through the SGTRs, and uncertainties in extrapolating to full scale the thermal-hydraulic parameters and results from the Semiscale SGTR/LBLOCA experiments.
According to the DRPS memorandum,1086 some of the 12 Semiscale (S-28) SGTR/ LBLOCA experiments indicated a PCT for a certain critical number of SGTRs. The experiments simulated the SGTRs by injecting flows at variable rates corresponding to single-ended ruptures of between 6 to 60 tubes. The two major conclusions from the Semiscale experiments were: (1) cladding temperatures do not reach a temperature necessary to compromise structural integrity of the PWR fuel rods; and (2) there is a narrow band of secondary-to-primary flow rates corresponding to between 12 to 20 SGTRs where the PCT reaches a high value of 1800F.
Basically, linear and volume scaling alternates were used in scaling the experiments, with each method having positive and negative features with respect to extrapolation to full scale geometries and thermal-hydraulic performances. The bottom line is that there is uncertainty in the SGTR flow rate scaling and modeling which would produce uncertainty in the PCT versus the number of ruptured tubes. Thus, the PCT versus the number of SGTRs in full scale reactors might shift to either lower, or higher, numbers of SGTRs. This would make the conclusions on the band of SGTRs (12 to 20 tubes) which produce a PCT in the Semiscale experiments questionable for extrapolation to actual reactors. However, simplified conservative estimates1086 have indicated that, within the assumptions applied, the PCTs for a LBLOCA coupled with SGTRs will most likely be below the (2200F) limit specified in 10 CFR 50.46.
Safety Significance
During a LBLOCA, consequential SGTRs may be induced by high depressurization loads and/or condensation-induced oscillations expected in the refill/reflood phases of the accident. Following the blowdown stage of a LBLOCA after the ECCS has been initiated and until the ECCS water fills the lower plenum, flow from the secondary side of a ruptured steam generator (SG) can follow two paths: (1) into the vessel upper plenum, through the lower plenum, the downcomer, and out the cold leg break; and (2) through the broken loop SG, through the RCP, and out the break. The distribution of the flow will depend on the hydraulic resistance along the paths. During this period, flow in the core is negative.
As the lower plenum is filled, the first path may be blocked. The water level in the downcomer rises and the reflood stage may begin. The reflood will start only if the upper plenum pressure increase due to flow resistance of Path 2 does not overcome the downcomer static head. Depending on the SGTR flow rate and the resistances in the SG and RCP in the broken loop, pressure can increase and result in reverse core flow which will retard the onset of the refill stage.
After reflood begins, vapor generation in the core will begin. This effect is equivalent to an increase in the rupture flow rate, both of which lead to an increase in upper plenum pressure. The increase in pressure will eventually decrease the reflood rate and increase PCTs.
After ECCS injection, the cold water (mostly from the intact loops) comes into contact with the steam flowing either from the core region through the downcomer or through the hot leg and the steam generator primary side. The resulting condensation has a balancing effect on the vessel upper head pressure by offsetting the upper plenum pressure increase due to the SGTR steam flowing into the vessel. Eventually, the amount of steam leaving the upper plenum and the escape path will depend on the upper plenum pressure, the condensation rate, and pressure losses in the steam generator loops. Therefore, depending on an uncertain critical number of SGTRs, retarded reflooding of the core with potential higher PCTs may result in core degradation.
Fission product releases from the degraded core with early containment failure due to overpressurization, or direct release paths (containment bypass) into the secondary side through the SGTRs and out secondary side relief valves, or failure to isolate containment may result in radiological risks greater than previously analyzed.
Possible Solution
Uncertainties in scale modeling of the SGTR/LBLOCA experimental results make it difficult to confidently extrapolate the Semiscale conclusions and results to full scale PWRs. It may not be possible to remove all the uncertainties associated with all the competing effects leading to increased or decreased PCTs from LBLOCA-induced SGTRs.
However, a possible solution may be to evaluate scaling methods and to assess the results of the evaluations against the experimental data used in the existing best estimate PWR safety codes. This possible solution is consistent with the scaling recommendations in Section 3.1.4 of NUREG-1230,1076 and could be factored into ongoing scaling studies and continuance of the thermal-hydraulic code assessment programs.
PRIORITY DETERMINATION
The core-melt frequency and radiological risks associated with LBLOCAs and consequential SGTRs were previously analyzed in NUREG-0844,681 which provided an estimated core-melt frequency of 3 x 10-8/RY and radiological risks in terms of latent fatalities. Based on these results, the NUREG-0844681 studies concluded that LBLOCAs with consequential SGTRs, and steam binding-induced delay in core reflood resulting in increased PCTs, were insignificant in terms of core-melt probability and radiological risks.
For purposes of this evaluation and the concerns raised in this issue, the NUREG-0844681 evaluation was compared with the results of this evaluation, taking into account the adjustments outlined below.
LBLOCA Frequency: In NUREG-0844,681 the LBLOCA frequency was estimated at 10-4/RY based on the LBLOCA frequency used in WASH-1400.16 Since the WASH-140016 study, considerable effort has been expended on determining the creditability and frequency of a design basis LBLOCA. Advances in technology have since led to an
acceptance of the leak-before-break concept as applied to large diameter high-quality piping such as that used in the primary coolant loops of PWRs. This acceptance has resulted in proposed modifications1087 to the GDC-4, 10 CFR 50, requirements for protection against dynamic effects of postulated pipe ruptures.
In this regard, LLNL evaluated elimination of postulated pipe ruptures from the design basis for nuclear power plants.1088 The frequency of large diameter primary coolant pipe breaks used in the UCID-203971088 analysis was based on a median frequency of 10-7/RY. The 10 and 90 percentile values were given as 2 x 10-9/RY and 7 x 10-6/RY, respectively. For purposes of this analysis, we will use a value of 10-5/RY as a conservative estimate of a LBLOCA initiating frequency. The UCID-203971088 use of the median (10-7/RY) value was identified as conservative for several reasons. The basis for supporting use of the median value will not be pursued in this analysis. However, the indicated conservatism in the LBLOCA frequency used in this analysis is approximately two orders of magnitude. Therefore, this conservatism, when used in combination with the probability of consequential SGTRs (discussed below) should bound uncertainties associated with potential higher conditional probabilities of SGTR/LBLOCA from operationally degraded SG tubes.
Conditional Probability of SGTR/LBLOCA: The probability of a SGTR, given a LBLOCA, was addressed in NUREG-0844681 and was based on the probability of rupturing SG tubes as a consequence of a main steamline break (MSLB). Since NRC-sponsored burst and collapse tests indicated that a LOCA is a less limiting load case than the MSLB, from the standpoint of inducing SGTRs, the following NUREG-0844681 conditional SGTR/LBLOCA probability estimates were considered conservative:
| P(1 SGTR/LBLOCA) | =0.034 |
| P(2 to 10 SGTR/LBLOCA) | =0.014 |
| P(>10 SGTR/LBLOCA) | =0.003 |
In NUREG-0844,681 the number of SGTRs during a LBLOCA that tended to inhibit the core reflood process, and thereby increase the PCT and core-melt frequency estimate, was in the range of 10 to 20 SG tubes. Therefore, NUREG-0844681 used the value of 3 x 10-3 as the conditional probability of SGTR/LBLOCA as the limiting case. These estimates are consistent with the Semiscale experimental results discussed earlier.
However, based on the uncertainty associated with the SGTR flow rate scaling and modeling (also discussed earlier), the full scale reactor may experience maximum PCTs from less than the 12 to 20 SGTRs. This analysis will base the limiting case on the conditional probability of 3.4 x 10-2, which corresponds to the probability of rupturing a single SG tube. Our basis for using the higher value single SGTR probability stems from the ECCS ineffectiveness and boron dilution effects described below.
ECCS Ineffectiveness: As discussed in NUREG-0844,681 analysis and experimental results do not indicate that a core-melt would occur during a SGTR/LBLOCA event. However, in NUREG-0844681 the probability that a core-melt might occur as a result of ineffective ECCS operations was assumed to be 0.1. This estimate was intended to bound plant-to-plant variations and uncertainties in other unidentified aspects of the ECCS responses to a LBLOCA. The above NUREG-0844681 estimate is approximately an order of magnitude higher than typical ECCS unavailabilities.
A fault tree model was developed to assess whether or not the ECCS ineffectiveness value of 0.1 (intended in NUREG-0844 to account for other aspects of the ECCS response) is sufficient to bound potential return to core critcality from boron dilution in the primary system due to SGTR secondary coolant flow intrusion. The top event of the fault tree being ECCS pump failures or ineffective ECCS flows resulting from the boron dilution effects discussed below.
For ECCS pump failures, we considered the probability of both pumps failing (P1P2), or a common mode failure of the ECCS pumps (P). Letting P1 = P2, the ECCS pump failure probability (without boron dilution) is:
Pfo = P2 + P
Assuming a typical ECCS pump flow rate (Fp = 3000 gpm) and the single-ended SGTR flow rate into the primary system (Fs = 300 gpm) the change (dilution) in boron density (D) is approximated as:
| where | D = Fp/(Fp + NFs) |
| N = number of SGTRs |
Therefore, a conservative estimate of the ECCS ineffectiveness due to boron dilution from N steam generator tube ruptures is approximated by:
(1-D) = N/(N + 10)
The above equations: (1) under-predict the boron density (D) because various (dependent on N) amounts of the SGTR flow can be expected to vaporize in the core region and therefore not contribute to ECCS flow dilution; and (2) over-predict the ECCS ineffectiveness (1-D) due to the previous under-prediction of (D). However, the above equations approximate the expected trend that, as N increases, the (1-D) parameter approaches unity. Thus for increasing N, the ECCS ineffectiveness due to boron dilution increases. The ECCS ineffectiveness for both pumps due to the boron dilution effect, or a failure of one pump and ineffective pump flow from the second pump, is expressed as (1-D)2 + P(1-D) or
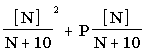
Summing the ECCS pump failures and ECCS ineffectiveness due to boron dilution effects yields an equation for the top event of the fault tree of:
| ECCS = P2 + | |
| where | P=0.1 (unavailability of one ECCS pump) |
Thus, without the boron dilution effect, the probability of ECCS unavailability (Pfo) is:
| Pfo | =P2 + |
| =0.02 |
However, the boron dilution effect is a function of the probability of N SGTRs. From the SGTR probabilities previously given, the probability of SGTRs (for N=1) can be approximated by:
| P(SGTR)=S1/N | |
| where | S1=0.034 (probability of one SGTR). |
The event tree sequences leading to potential core-melt (CM) from SGTRs/LBLOCA and ECCS independent or dependent failures or ineffective ECCS flows from the boron dilution effects yield the following expression:
| CM=(LBLOCA)(S1/N)[P2 + | |
| where | LBLOCA=Large-Break LOCA Frequency |
Prior to evaluating the above CM expression, a brief discussion of the postulated progression of the event should clarify the basis for the expression and the ECCS ineffectiveness as approximated in this analysis. It should be recognized that the above expression is a simplified probabilistic approximation of an extremely complex progression that is used herein only to compare with (test) the ECCS ineffectiveness value used in NUREG-0844:681
(1) During the refill and reflood retardation phases described earlier, the SGTR downflow in the core will be mostly vaporized with a void fraction greater then 10%. Under these moderator (steam) conditions, the core can be expected to remain subcritical. The ECCS and SGTR flows provide effective cooling and boron dilution is not a factor.
(2) During and following the reflood phase, the core can be expected to remain subcritical with xenon, all control rods in, and 200F coolant, if the boron concentrations range above 300 to 500 ppm. The ECCS and SGTR flows provide effective cooling if the core remains subcritical. However, the potential for boron dilution from SGTRs should be considered during this phase because a return to criticality could heat up the core, increase upper plenum pressure, and depress the reflood by expelling coolant out the break (ineffective in-flow of ECCS). Under these conditions, flow oscillations in the core and potential core degradation may occur.
The above boron dilution scenario could, however, be limited by many variables such as: (1) the availability of secondary coolant inventory; (2) the location of the SGTRs; (3) the pressure balancing between the primary and secondary systems; and (4) the resistance in the flow paths of the broken loop.
By setting [D = 10/(N + 10)] equal to ratios of subcritical boron concentrations (ranging from 300 to 500 ppm) and an ECCS boron concentration of 2000 ppm, we solve for the range of SGTRs (N) that are estimated to approach critical boron dilution concerns. Based on these calculations, we estimate that between 30 to 60 SGTRs would be required for departure from subcriticality due to SGTR secondary coolant intrusion.
Inputting a median value of N = 45 into the equation for CM, and in the limit resetting D = 0, yields (to two decimal places) a simplified expression of:
CM = (LBLOCA)(0.02)(S1)
The above results indicated that ECCS ineffectiveness would increase with increasing numbers of SGTRs. However, the decreasing probability of multiple SGTRs decreases at a faster rate than the increasing dilution effect. Thus the value of 0.1 used in NUREG-0844681 as an estimate of potential ECCS ineffectiveness, when compared to the conservative probabilistically-weighted ECCS boron dilution from SGTRs, may bound the dilution effect by approximately an order of magnitude.
In the following analysis, we will use the more conservative value (0.1) as used in NUREG-0844681 in lieu of the value of 0.02 calculated above. Thus, with the conservatisms inherent in the methodology and input values, this analysis should yield an upper bound for the concerns of this issue.
Frequency Estimate
Based on the above discussions and estimates, the core-melt frequency estimated in NUREG-0844681 is compared to the core-melt frequency for this issue, which is adjusted to account for the concerns identified and evaluated.
| Event | NUREG-0844 | This Analysis |
|---|---|---|
| LBLOCA | 1 x 10-4/RY | 1.0 x 10-5/RY |
| Limiting SGTR/LBLOCA | 3 x 10-3 | 3.4 x 10-2 |
| ECCS Ineffectiveness | 1 x 10-1 | 1.0 x 10-1 |
| Core-melt Frequency | 3 x 10-8/RY | 3.4 x 10-8/RY |
From the above estimates, the core-melt frequency due to concurrent LBLOCAs and SGTRs, accompanied by steam binding-induced delay in core reflood, is extremely low. It is also noted that the initiating LBLOCA frequency which drives this event may be conservative by approximately two orders of magnitude and the boron dilution effect may also be overestimated by approximately an order of magnitude. Therefore, the above estimates should bound any nonconservatism that may arise from operational degraded SG tubes.
Containment Failure Modes
Three potential containment failure modes are considered for this issue: (1) early containment failure due to overpressure; (2) containment bypass due to radiological releases through the ruptured SG tubes and secondary relief valves, or failure to isolate containment; and (3) basemat melt-through. In all cases, containment sprays and fan coolers are assumed operable. The probability of early containment failure for a LBLOCA with SGTRs is 0.07 (NUREG-1150,1081 Bin 11, Tables C.6 and C.7). For purposes of this analysis, we will use a value of 0.1.
The above postulated paths through the secondary relief valves, or failure to isolate containment, are containment bypass radiological releases. For this event (SGTRs/LBLOCA) we would not expect the secondary side relief valves to be challenged (opened) or therefore to stick open following the event. We would also not expect the probability of failure to isolate containment to exceed 0.1. However, to bound the concern1086 associated with potential direct release paths via the secondary side, we will conservatively use the 0.3 probability of containment bypass from SGTRs accompanied by stuck-open secondary relief valves from NUREG-1150 (Bin 17, Tables D.7 and D.8).1081 If the containment does not fail by overpressurization or containment bypass, it is assumed to fail by basemat melt-through.
Consequence Estimate
The conditional release doses used in this analysis are based on the fission product inventory of a 1120 MWe PWR plant, meteorology typical of a midwest site, a surrounding uniform population density of 340 persons per square mile within a 50-mile radius of the plant, an exclusion radius of one-half mile, no evacuation, and no ingestion pathways. Therefore, the estimated risk reduction potential is representative of a hypothetical generic PWR plant and not representative of any specific plant. The radiological release categories are as defined in WASH-1400.16 The estimated potential risk reduction shown in Table 3.141-1 are in terms of man-rem/RY and man-rem/reactor (assuming a remaining plant life of 30 years).
| TABLE 3.141-1 Risk Summary | ||||
|---|---|---|---|---|
| Core-Melt Frequency (CM/RY) | Containment Failure Probability (CF/CM) | Dose (man-rem per CF) | Public Risk (man-rem/RY) | Public Risk (man-rem/R) |
| 3.4 x 10-8 | 0.1 | Cat. 3 5.4 x 106 | 0.02 | 0.6 |
| 3.4 x 10-8 | 0.3 | Cat. 5 1.0 x 106 | 0.01 | 0.3 |
| 3.4 x 10-8 | 0.6 | Cat. 7 2.3 x 103 | - | - |
| TOTAL | - | - | 0.03 | 0.9 |
Cost Estimate
Because of the low risks associated with this issue, no cost estimate was developed; costs will not affect the priority ranking.
Value/Impact Assessment
Because of the low risk reduction and the absence of any cost estimate, a value/ impact assessment for this issue was not provided. The value/impact score will not affect the priority ranking.
CONCLUSION
This issue was raised as a GSI because of uncertainties in the scaling models developed from semiscale experimental testing of LBLOCAs accompanied by SGTRs. From the semiscale results, two major conclusions were reached: (1) the PCT does not reach a temperature necessary to compromise structural integrity of the PWR fuel rods; and (2) the critical number of SGTRs necessary to reach the maximum PCT numbers between 12 to 20 SGTRs. The principal concerns upon which this issue was raised are centered around Conclusion 2 from the semiscale tests and boron dilution of the ECCS coolant. Due to the uncertainties in extrapolating the semiscale results to full-scale reactors, the concern was that the critical number of SGTRs following a LBLOCA could shift to lower, or higher, numbers of SGTRS. Because it is more likely that lower numbers of STGRs could occur following a LBLOCA, this analysis focused on this aspect of the concern and the potential probabilistically-weighted boron dilution of the ECCS coolant.
In consideration of the above concerns, the core-melt frequency for a LBLOCA with an SGTR was estimated to be 3.4 x 10-8/RY thus making the issue a low priority. The potential risk reduction, based on the conservative core-melt frequency, was estimated to be 0.9 man-rem/reactor. Because of the low core-melt frequency and low potential risk reduction, no cost estimate or value/ impact score was made. These estimates, if made, would not affect the priority ranking of the issue. Thus, this issue was DROPPED from further consideration.
REFERENCES
|


